Brainwave

What is Brainwave Entrainment

---

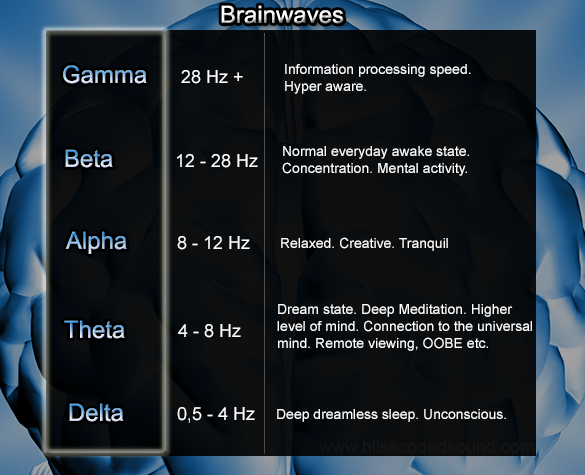
Beta waves are characteristics of a strongly engaged mind. A person in active conversation would be in beta. A debater would be in high beta. A person making a speech, or a teacher, or a talk show host would all be in beta when they are engaged in their work. Where beta represented arousal, alpha represents non-arousal. Alpha brainwaves are slower, and higher in amplitude. Their frequency ranges from 9 to 14 cycles per second. A person who has completed a task and sits down to rest is often in an alpha state. A person who takes time out to reflect or meditate is usually in an alpha state.

A person who takes a break from a conference and walks in the garden is often in an alpha state. The next state, theta brainwaves, are typically of even greater amplitude and slower frequency. This frequency range is normally between 5 and 8 cycles a second. A person who has taken time off from a task and begins to daydream is often in a theta brainwave state.

A person who is driving on a freeway, and discovers that they can't recall the last five miles, is often in a theta state--induced by the process of freeway driving. The repetitious nature of that form of driving compared to a country road would differentiate a theta state and a beta state in order to perform the driving task safely. Individuals who do a lot of freeway driving often get good ideas during those periods when they are in theta. Individuals who run outdoors often are in the state of mental relaxation that is slower than alpha and when in theta, they are prone to a flow of ideas.

This can also occur in the shower or tub or even while shaving or brushing your hair. It is a state where tasks become so automatic that you can mentally disengage from them. The ideation that can take place during the theta state is often free flow and occurs without censorship or guilt.

These rhythmic changes in membrane potential do not reach the critical threshold and therefore do not result in an action potential. They can result from postsynaptic potentials from synchronous inputs or from intrinsic properties of neurons. Neuronal spiking can be classified by their activity patterns. The excitability of neurons can be subdivided in Class I and II. Class I neurons can generate action potentials with arbitrarily low frequency depending on the input strength, whereas Class II neurons generate action potentials in a certain frequency band, which is relatively insensitive to changes in input strength.

A group of neurons can also generate oscillatory activity. Through synaptic interactions the firing patterns of different neurons may become synchronized and the rhythmic changes in electric potential caused by their action potentials will add up constructive interference.

Neural oscillation

That is, synchronized firing patterns result in synchronized input into other cortical areas, which gives rise to large-amplitude oscillations of the local field potential. These large-scale oscillations can also be measured outside the scalp using electroencephalography EEG and magnetoencephalography MEG. The electric potentials generated by single neurons are far too small to be picked up outside the scalp, and EEG or MEG activity always reflects the summation of the synchronous activity of thousands or millions of neurons that have similar spatial orientation.

Instead, the probability of firing is rhythmically modulated such that neurons are more likely to fire at the same time, which gives rise to oscillations in their mean activity see figure at top of page. As such, the frequency of large-scale oscillations does not need to match the firing pattern of individual neurons. Isolated cortical neurons fire regularly under certain conditions, but in the intact brain cortical cells are bombarded by highly fluctuating synaptic inputs and typically fire seemingly at random.

However, if the probability of a large group of neurons is rhythmically modulated at a common frequency, they will generate oscillations in the mean field see also figure at top of page. In particular, inhibitory interneurons play an important role in producing neural ensemble synchrony by generating a narrow window for effective excitation and rhythmically modulating the firing rate of excitatory neurons. Neural oscillation can also arise from interactions between different brain areas coupled through the structural connectome. Time delays play an important role here.

Because all brain areas are bidirectionally coupled, these connections between brain areas form feedback loops. Positive feedback loops tends to cause oscillatory activity where frequency is inversely related to the delay time. An example of such a feedback loop is the connections between the thalamus and cortex — the thalamocortical radiations.

This thalamocortical network is able to generate oscillatory activity known as recurrent thalamo-cortical resonance. Scientists have identified some intrinsic neuronal properties that play an important role in generating membrane potential oscillations. In particular, voltage-gated ion channels are critical in the generation of action potentials. The dynamics of these ion channels have been captured in the well-established Hodgkin—Huxley model that describes how action potentials are initiated and propagated by means of a set of differential equations.

Using bifurcation analysis , different oscillatory varieties of these neuronal models can be determined, allowing for the classification of types of neuronal responses. The oscillatory dynamics of neuronal spiking as identified in the Hodgkin—Huxley model closely agree with empirical findings. In addition to periodic spiking, subthreshold membrane potential oscillations , i.

Bursting neurons have the potential to serve as pacemakers for synchronous network oscillations, and bursts of spikes may underlie or enhance neuronal resonance. Apart from intrinsic properties of neurons, biological neural network properties are also an important source of oscillatory activity. Neurons communicate with one another via synapses and affect the timing of spike trains in the post-synaptic neurons.

Depending on the properties of the connection, such as the coupling strength, time delay and whether coupling is excitatory or inhibitory , the spike trains of the interacting neurons may become synchronized. Certain network structures promote oscillatory activity at specific frequencies. For example, neuronal activity generated by two populations of interconnected inhibitory and excitatory cells can show spontaneous oscillations that are described by the Wilson-Cowan model. If a group of neurons engages in synchronized oscillatory activity, the neural ensemble can be mathematically represented as a single oscillator.

Weakly coupled oscillators can generate a range of dynamics including oscillatory activity. Because most connections are reciprocal, they form feed-back loops that support oscillatory activity. Oscillations recorded from multiple cortical areas can become synchronized to form large scale brain networks , whose dynamics and functional connectivity can be studied by means of spectral analysis and Granger causality measures. In addition to fast direct synaptic interactions between neurons forming a network, oscillatory activity is regulated by neuromodulators on a much slower time scale.

That is, the concentration levels of certain neurotransmitters are known to regulate the amount of oscillatory activity. For instance, GABA concentration has been shown to be positively correlated with frequency of oscillations in induced stimuli.

You are here

These neurotransmitter systems affect the physiological state, e. Oscillations can often be described and analyzed using mathematics. Mathematicians have identified several dynamical mechanisms that generate rhythmicity. Among the most important are harmonic linear oscillators, limit cycle oscillators, and delayed- feedback oscillators. They generally arise when a physical system is perturbed by a small degree from a minimum-energy state , and are well understood mathematically. Noise-driven harmonic oscillators realistically simulate alpha rhythm in the waking EEG as well as slow waves and spindles in the sleep EEG.

Successful EEG analysis algorithms were based on such models. Several other EEG components are better described by limit-cycle or delayed-feedback oscillations. Limit-cycle oscillations arise from physical systems that show large deviations from equilibrium , whereas delayed-feedback oscillations arise when components of a system affect each other after significant time delays.

Limit-cycle oscillations can be complex but there are powerful mathematical tools for analyzing them; the mathematics of delayed-feedback oscillations is primitive in comparison. Linear oscillators and limit-cycle oscillators qualitatively differ in terms of how they respond to fluctuations in input. In a linear oscillator, the frequency is more or less constant but the amplitude can vary greatly.

In a limit-cycle oscillator, the amplitude tends to be more or less constant but the frequency can vary greatly. A heartbeat is an example of a limit-cycle oscillation in that the frequency of beats varies widely, while each individual beat continues to pump about the same amount of blood.

Computational models adopt a variety of abstractions in order to describe complex oscillatory dynamics observed in brain activity. Many models are used in the field, each defined at a different level of abstraction and trying to model different aspects of neural systems.

They range from models of the short-term behaviour of individual neurons, through models of how the dynamics of neural circuitry arise from interactions between individual neurons, to models of how behaviour can arise from abstract neural modules that represent complete subsystems. A model of a biological neuron is a mathematical description of the properties of nerve cells, or neurons, that is designed to accurately describe and predict its biological processes. The most successful and widely used model of neurons, the Hodgkin—Huxley model, is based on data from the squid giant axon.

Get smart. Sign up for our email newsletter.

It is a set of nonlinear ordinary differential equations that approximates the electrical characteristics of a neuron, in particular the generation and propagation of action potentials. The model is very accurate and detailed and Hodgkin and Huxley received the Nobel Prize in physiology or medicine for this work.

The mathematics of the Hodgkin—Huxley model are quite complicated and several simplifications have been proposed, such as the FitzHugh—Nagumo model and the Hindmarsh—Rose model. Such models only capture the basic neuronal dynamics, such as rhythmic spiking and bursting , but are more computationally efficient. This allows the simulation of a large number of interconnected neurons that form a neural network. A neural network model describes a population of physically interconnected neurons or a group of disparate neurons whose inputs or signalling targets define a recognizable circuit.

These models aim to describe how the dynamics of neural circuitry arise from interactions between individual neurons. Local interactions between neurons can result in the synchronization of spiking activity and form the basis of oscillatory activity. In particular, models of interacting pyramidal cells and inhibitory interneurons have been shown to generate brain rhythms such as gamma activity. Neural field models are another important tool in studying neural oscillations and are a mathematical framework describing evolution of variables such as mean firing rate in space and time.

In modeling the activity of large numbers of neurons, the central idea is to take the density of neurons to the continuum limit, resulting in spatially continuous neural networks. Instead of modelling individual neurons, this approach approximates a group of neurons by its average properties and interactions. It is based on the mean field approach , an area of statistical physics that deals with large-scale systems. Models based on these principles have been used to provide mathematical descriptions of neural oscillations and EEG rhythms.

They have for instance been used to investigate visual hallucinations.

The Kuramoto model of coupled phase oscillators [36] is one of the most abstract and fundamental models used to investigate neural oscillations and synchronization. It captures the activity of a local system e. The Kuramoto model is widely used to study oscillatory brain activity and several extensions have been proposed that increase its neurobiological plausibility, for instance by incorporating topological properties of local cortical connectivity. Simulations using the Kuramoto model with realistic long-range cortical connectivity and time-delayed interactions reveal the emergence of slow patterned fluctuations that reproduce resting-state BOLD functional maps, which can be measured using fMRI.

What is the function of the various brainwaves?

Both single neurons and groups of neurons can generate oscillatory activity spontaneously. In addition, they may show oscillatory responses to perceptual input or motor output. Some types of neurons will fire rhythmically in the absence of any synaptic input. Likewise, brain-wide activity reveals oscillatory activity while subjects do not engage in any activity, so-called resting-state activity.

These ongoing rhythms can change in different ways in response to perceptual input or motor output. Oscillatory activity may respond by increases or decreases in frequency and amplitude or show a temporary interruption, which is referred to as phase resetting. What is Brainwave Entrainment. Brainwave entrainment is a method to stimulate the brain into entering a specific state by using a pulsing sound, light, or electromagnetic field.

On the positive side, this same mechanism is commonly used to induce many brainwave states; such as a trance, enhanced focus, relaxation, meditation or sleep induction. The brainwave entrainment effectively pushes the entire brain into a certain state. Brainwave entrainment works for almost everyone. It is a great way to lead your mind into states that you might usually have difficulty reaching, allowing you to experience what those states feel like.

Any stable frequency evokes a cortical response. The brain synchronises its dominant brainwave frequency with that of the external stimulus. This is called Brainwave Entrainment. There is a lot of marketing hype around brainwave entrainment.

• The Invention of Deconstruction
• HERE WITHOUT YOU: SCRIPT
• The PMO Best Practices: Launching Products for Market Success (The PMO Practice Booklet Book 5)
• Smart Cameras
• A.D.A,M. Interactive Anatomy Online Student Lab Activity Guide
• Voyages From Montreal Through the Continent of North America to the Frozen and Pacific Oceans in 1789 and 1793 (Complete)