Strength of Materials Von Mises Stress
Contents:
Rheology Viscoelasticity Rheometry Rheometer. Discovering a generalized criterion that can predict the mechanical failure of various different structural materials is one of ultimate goals for scientists in both material and mechanics communities. China Find articles by Z. History of Strength of Materials. Laws Conservations Energy Mass Momentum. In this case, Eq. From Wikipedia, the free encyclopedia.
Data points were plotted based on data in Supplementary Tables S1—S3. Note that the outline of each material zone is not the accurate boundary of the corresponding material kind, only embracing the current data points and suggesting a trend. In conclusion, this work proposes a generalized energy criterion for predicting the failure of materials, which is particularly applicable for the materials with comparable energy barriers for shear and cleavage, such as MGs, NC and UFG materials 23 , 24 , 25 , 26 , 27 , 28 , Quantitative experiment confirms the validity of the proposed generalized energy criterion for predicting the tensile failure of MG.
Based on the energy criterion, the intrinsic failure mechanism map of materials is quantitatively established, which explicitly gives an exhibition and also a prediction of the failure mode of each kind of materials.
von Mises yield criterion
The generalized energy criterion is consistent with the classical approaches of mechanics for predicting failure via energy methods, but provides new physical insights into the failure criterion by considering the inherent failure mechanism of materials. We selected an MG with a composition of Zr The amorphous structure of the specimens was identified by standard X-ray diffraction. In the fracture-controlled tensile tests, fracture was controlled to occur along the designed planes with different angles with respect to the loading axis, by means of introducing inclined notches to dog-bone specimens.
Smooth specimens without notches were also prepared to measure the tensile strength and observe the fracture features. Hence the fractures of inclined notch tensile specimens were well controlled and occurred along the designed notch planes see Fig. How to cite this article: Generalized energy failure criterion. All authors discussed the results for many times. National Center for Biotechnology Information , U. Published online Mar Zhang , 1 P. Zhang , 1 Z.
Navigation menu
China Find articles by R. China Find articles by Z. China Find articles by P. Author information Article notes Copyright and License information Disclaimer. Received Nov 23; Accepted Mar 4. This work is licensed under a Creative Commons Attribution 4. To view a copy of this license, visit http: This article has been cited by other articles in PMC.
Abstract Discovering a generalized criterion that can predict the mechanical failure of various different structural materials is one of ultimate goals for scientists in both material and mechanics communities. Open in a separate window.
Reduced von Mises equation for different stress conditions
Illustrations on the two basic failure mechanisms of material. Results The energy basis of the above failure criteria and the energy criterion for crack propagation suggest that the failure of materials may be generally dominated by energy.
Therefore, to predict various different materials, it is necessary to consider both the shear and cleavage mechanisms for the failure, and the following generalized energy criterion may be proposed: Tensile fracture features and failure mechanism of a typical Zr-based MG. Experimental results of controlled tensile fracture of Vit MG 10 , Energy diagram for the tensile failure of Vit MG.
Discussion Like the Tresca criterion and the Rankine criterion, the present energy criterion can also be written in the form of stresses. Application for predicting the failure As a failure criterion, the generalized energy criterion can be employed to predict the critical conditions for failure of materials or structural component at complex stress states.
For isotropic materials e.
- Rockstar Dreams (Rockstar Erotic Romance #3) (Rockstar Erotic Romance Series).
- Von Mises Stress.
- Associated Data.
- Bound to Serve (Nexus)!
- Digital Design and Computer Architecture: From Gates to Processors.
- Maximum von Mises Stress Criterion?
- Little Blue Book Advent and Christmas Seasons 2011-2012.
In this case, we can apply the criterion to predict the failure conditions according to the following procedure. Under uniaxial tension, the material also tends to yield first; thus the elastic strain energy density for yielding under uniaxial tension, E Ty , should not be the energy barrier for cleavage fracture, E c0. However, since the failure happens with the minimum energy input, we can make the measured E Ty equal to the E Tmin predicted by the present energy criterion according to Eq.
On the other hand, if the material is brittle and cleavage fracture occurs before yielding, the elastic strain energy density for fracture under uniaxial tension should be the energy barrier for cleavage fracture, i. However, for brittle materials even under simple shear, the fracture may still be controlled by cleavage fracture, thus the E s0 cannot be directly measured by simple shear test.
In this case, double shear test can be done. By introducing shear stress in another direction, the fracture mode will become a mixed mode of shear and cleavage. Through measuring the fracture angle and fracture stress, the E s0 can be finally determined. For example, for the stress state of uniaxial tension, we can directly use Eqs 12 , 13 , 14 , 15 , 16 , 17 to calculate the stresses and energy densities, while for other cases a careful stress analysis may be required.
For instance, Eqs 20 , 21 are the predicted results for failure of isotropic materials under tension. For anisotropic materials e. To apply the present criterion, we need firstly to find all kinds of planes, and then determine the two energy barriers for failure E s0 and E c0 of each plane. Since the anisotropy, some special designed experiments may be required, which can be referred to the studies on the failure criterion of composite materials 3. Similar to the above procedure, the shear and normal stresses on the possible planes require to be calculated by stress analysis, and then the associated energy density can be obtained.
The energy criterion will be applied for all kinds of planes, while the failure conditions including the failure plane and the failure stress should correspond to the plane that failure occurs requiring the minimum total input energy. The application of the energy criterion to anisotropic materials still requires further investigations, including experimental validations. Establishment of the intrinsic failure mechanism map As discussed above, the present energy criterion includes the contributions from both of the two basic failure mechanisms, thus is expected to predict the failure of a broad range of materials from ductile to brittle.
The von Mises yield criterion suggests that yielding of a ductile .. reaches the yield strength of the material in simple tension, σ y {\displaystyle \sigma _{y}} \ sigma_y. As an example, the stress state. Strength / Mechanics of Materials Table of Contents In this case, a material is said to start yielding when its von Mises stress reaches a critical value known as .
Intrinsic failure mechanism map of materials. Methods We selected an MG with a composition of Zr Additional Information How to cite this article: This implies that the yield condition is independent of hydrostatic stresses. The above equation can be reduced and reorganized for practical use in different loading scenarios.
In the case of uniaxial stress or simple tension , , the von Mises criterion simply reduces to. It is also convenient to define an Equivalent tensile stress or von Mises stress , , which is used to predict yielding of materials under multiaxial loading conditions using results from simple uniaxial tensile tests. In this case, yielding occurs when the equivalent stress, , reaches the yield strength of the material in simple tension,.
As an example, the stress state of a steel beam in compression differs from the stress state of a steel axle under torsion, even if both specimens are of the same material. In view of the stress tensor, which fully describes the stress state, this difference manifests in six degrees of freedom , because the stress tensor has six independent components.
von Mises yield criterion
Therefore, it is difficult to tell which of the two specimens is closer to the yield point or has even reached it. However, by means of the von Mises yield criterion, which depends solely on the value of the scalar von Mises stress, i. A larger von Mises value implies that the material is closer to the yield point. In the case of pure shear stress , , while all other , von Mises criterion becomes:.
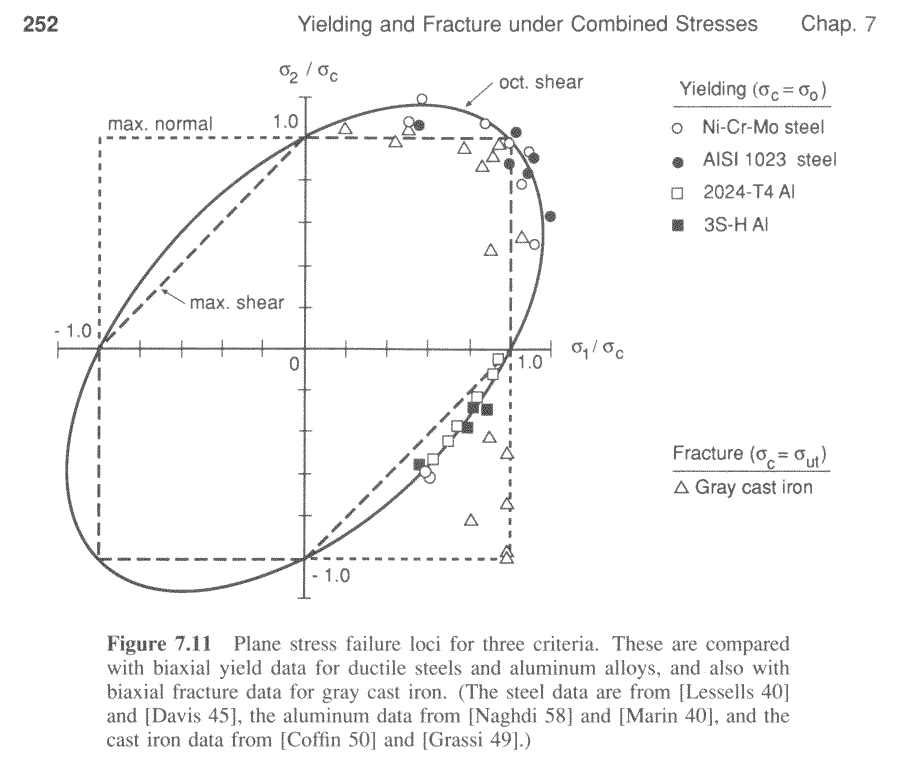
This means that, at the onset of yielding, the magnitude of the shear stress in pure shear is times lower than the tensile stress in the case of simple tension. The von Mises yield criterion for pure shear stress, expressed in principal stresses, is. In the case of plane stress , , the von Mises criterion becomes:. This equation represents an ellipse in the plane , as shown in the Figure above. Sign up or log in Sign up using Google.
Sign up using Facebook. Sign up using Email and Password. Post as a guest Name. Email Required, but never shown. Post Your Answer Discard By clicking "Post Your Answer", you acknowledge that you have read our updated terms of service , privacy policy and cookie policy , and that your continued use of the website is subject to these policies. Physics Stack Exchange works best with JavaScript enabled.